O que são Produtos Notáveis? Guia do Quadrado da Soma e Diferença

Na álgebra, que começamos a explorar ao resolver equações de primeiro grau, encontramos certas multiplicações que aparecem com tanta frequência que ganharam um nome especial: produtos notáveis.

Basicamente, são “padrões” de multiplicação. Se você aprender a reconhecê-los, você não precisará fazer o cálculo longo (o “chuveirinho” ou distribuição) toda vez. Portanto, dominar os produtos notáveis é como ter um atalho lógico para chegar à solução mais rápido.

O Método Lento (Sem o Atalho): A Propriedade Distributiva

Primeiramente, vamos ver o que acontece quando não usamos o atalho.
Se quisermos calcular (x + 3)², o que isso significa? Significa (x + 3) multiplicado por ele mesmo: (x + 3) * (x + 3).

Para resolver isso, usamos a propriedade distributiva (o “chuveirinho”):
1. x * x = x²
2. x * 3 = 3x
3. 3 * x = 3x
4. 3 * 3 = 9

Agora, juntamos os termos: x² + 3x + 3x + 9
Resultado: x² + 6x + 9

O método funciona, mas é trabalhoso. Agora, vamos aplicar a lógica do padrão.

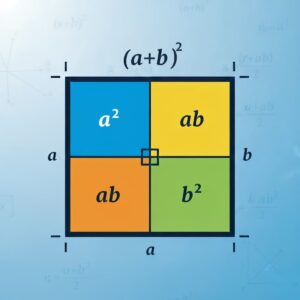
Produto Notável 1: O Quadrado da Soma (a + b)²

O (x + 3)² é um exemplo perfeito do “Quadrado da Soma”. A forma geral é (a + b)².
A lógica (o padrão) é sempre a mesma:
(a + b)² = a² + 2ab + b²

Vamos traduzir isso para o português:
“O quadrado do primeiro termo, mais duas vezes o primeiro termo pelo segundo, mais o quadrado do segundo termo.”

Vamos aplicar essa regra ao nosso (x + 3)², onde ‘a’ = x e ‘b’ = 3:
1. O quadrado do primeiro (x²): x²
2. Mais duas vezes o primeiro (x) pelo segundo (3): 2 * x * 3 = 6x
3. Mais o quadrado do segundo (3²): 9

Resultado: x² + 6x + 9
Chegamos à mesma resposta, mas em um único passo, sem distribuição.

Produto Notável 2: O Quadrado da Diferença (a – b)²

A lógica é quase idêntica, contudo, o sinal do meio muda.
A forma geral é (a – b)².
(a – b)² = a² – 2ab + b²

A regra:
“O quadrado do primeiro termo, menos duas vezes o primeiro termo pelo segundo, mais o quadrado do segundo termo.”

Exemplo: Calcular (x – 5)². (Aqui, ‘a’ = x e ‘b’ = 5)
1. O quadrado do primeiro (x²): x²
2. Menos duas vezes o primeiro (x) pelo segundo (5): -2 * x * 5 = -10x
3. Mais o quadrado do segundo (5²): 25

Resultado: x² – 10x + 25

Atenção: Note que o último termo (+25) é positivo, pois (-5) * (-5) dá +25, conforme as regras de sinais.

Bônus: Produto da Soma pela Diferença (a + b)(a – b)

Este é outro padrão muito comum. Quando você multiplica a soma de dois termos pela diferença desses mesmos termos, o resultado é ainda mais simples:
(a + b) * (a – b) = a² – b²

A regra: “O quadrado do primeiro termo menos o quadrado do segundo termo.”
Exemplo: (x + 7) * (x – 7) = x² – 7² = x² – 49.

Conclusão: Pense Fora da Caixa e Use os Padrões

Como você pode ver, os produtos notáveis não são fórmulas mágicas para decorar. São padrões lógicos. Ao invés de usar a força bruta da distribuição (chuveirinho) toda vez, você pode pensar fora da caixa e resolver o problema reconhecendo o padrão e aplicando o atalho.

Isso é fundamental para o próximo passo da álgebra: a Fatoração (que é o caminho inverso dos produtos notáveis).

A Matemática é a linguagem do universo, vamos dominá-la!