Números Inteiros e Regras de Sinais: O Guia Lógico (Adição, Subtração e Multiplicação)
Um dos maiores saltos lógicos do 6º para o 7º ano é a introdução dos números inteiros, ou seja, os números negativos. Consequentemente, dominar as regras de sinais (também conhecido como “jogo de sinais”) torna-se uma ferramenta essencial para toda a matemática futura, incluindo a resolução de equações.
Muitos alunos tentam apenas decorar as regras, mas isso leva a erros. No entanto, a matemática não é sobre decoração, é sobre lógica. Assim como aprendemos a lógica da porcentagem, hoje vamos encontrar a lógica por trás das operações com números negativos.
O que são Números Inteiros? A Lógica da Reta Numérica
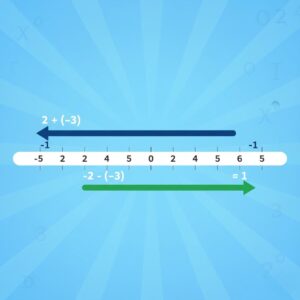
Primeiramente, vamos visualizar o problema. Os números inteiros são todos os números positivos, os negativos e o zero. A melhor forma de entendê-los é através da reta numérica.
- O Zero (0) é o centro (a origem).
- À direita, temos os números positivos (1, 2, 3…).
- À esquerda, temos os números negativos (-1, -2, -3…).
Pense fora da caixa e resolva o problema visualizando: “Adicionar” significa “andar para a direita” e “Subtrair” significa “andar para a esquerda”.
Regras de Sinais para Adição e Subtração (A Lógica da Dívida)
Esta é a parte que mais confunde, pois o “jogo de sinais” (mais com mais, menos com menos) NÃO SE APLICA AQUI.
Para adição e subtração, a lógica mais fácil é a do “dinheiro”:
- Números Positivos (+) = Dinheiro que você TEM.
- Números Negativos (-) = Dinheiro que você DEVE.
O resultado da operação é o seu saldo final.
Caso 1: Sinais Iguais (Soma ou Dívida Acumulada)
(+5) + (+2) = Você tem 5 e ganha 2. Logo, você tem 7 (+7).
(-5) + (-2) = Você deve 5 e faz outra dívida de 2. Logo, você deve 7 (-7).
Lógica: Sinais iguais, some os valores e mantenha o sinal.
Caso 2: Sinais Diferentes (Abatimento da Dívida)
(+7) + (-3) = Você tem 7, mas deve 3. Você paga a dívida. Logo, você fica com 4 (+4).
(-10) + (+4) = Você deve 10, mas tem 4. Você paga parte da dívida. Logo, você continua devendo 6 (-6).
Lógica: Sinais diferentes, subtraia os valores (o maior pelo menor) e mantenha o sinal do “número maior” (o que você tinha mais: dívida ou dinheiro).
O Caso Especial: Subtração de Número Negativo
O que significa (-5) – (-3)?
Aqui, usamos a lógica do “oposto”. O sinal de menos (-) antes do parêntese significa “o oposto de”.
Portanto, (-5) – (-3) é o mesmo que (-5) + (o oposto de -3).
O oposto de -3 é +3.
A conta vira: (-5) + (+3).
Usando a lógica da dívida: Você deve 5, mas tem 3. Você paga parte. Logo, você fica devendo 2 (-2).
Regras de Sinais para Multiplicação e Divisão (O Verdadeiro “Jogo de Sinais”)
Aqui sim, usamos o famoso “Jogo de Sinais”. A lógica é binária (simples) e se aplica igualmente para multiplicação (x) e divisão (÷).
- Sinais IGUAIS sempre resultam em POSITIVO (+).
- (+) x (+) = +
- (-) x (-) = +
- Sinais DIFERENTES sempre resultam em NEGATIVO (-).
- (+) x (-) = –
- (-) x (+) = –
Exemplos de Multiplicação:
(+5) x (+3) = +15 (Sinais iguais = Positivo)
(-5) x (-3) = +15 (Sinais iguais = Positivo)
(-5) x (+3) = -15 (Sinais diferentes = Negativo)
(+5) x (-3) = -15 (Sinais diferentes = Negativo)
Exemplos de Divisão:
(+10) ÷ (+2) = +5 (Sinais iguais = Positivo)
(-10) ÷ (-2) = +5 (Sinais iguais = Positivo)
(-10) ÷ (+2) = -5 (Sinais diferentes = Negativo)
(+10) ÷ (-2) = -5 (Sinais diferentes = Negativo)

Conclusão: Duas Lógicas Diferentes
Portanto, o erro mais comum é confundir as duas lógicas. As regras de sinais não são universais.
1. Para Adição e Subtração: Use a lógica da Dívida e Dinheiro (sinais iguais somam, sinais diferentes subtraem).
2. Para Multiplicação e Divisão: Use o Jogo de Sinais (iguais dão +, diferentes dão -).
Separe esses dois conceitos em sua mente, e você dominará os números inteiros. A Matemática é a linguagem do universo, vamos dominá-la!