Área e Perímetro: Qual a Diferença? (Um Guia de Geometria Plana)
Na geometria, duas das medições mais fundamentais são área e perímetro. Frequentemente, os alunos confundem esses dois conceitos, mas eles medem coisas fundamentalmente diferentes. Saber qual é qual é tão crucial quanto dominar a regra de três simples para resolver problemas.
Portanto, o objetivo deste guia é estabelecer, de forma lógica e definitiva, a diferença entre eles, como calculá-los e quando usar cada um.
Perímetro: A Lógica do Contorno
Primeiramente, vamos definir o Perímetro. Pense fora da caixa e resolva o problema com uma analogia simples: o perímetro é a cerca ao redor de um terreno, o rodapé de uma sala ou o contorno da figura.
Em outras palavras, o perímetro é a soma de todos os lados de uma figura plana. É uma medida de comprimento (unidimensional), por isso usamos unidades como centímetros (cm), metros (m) ou quilômetros (km).
Exemplo 1: Quadrado
Um quadrado com lado de 5 cm.
Perímetro = 5 + 5 + 5 + 5 (ou 4 x 5)
Perímetro = 20 cm
Exemplo 2: Retângulo
Um retângulo com base de 10 cm e altura de 3 cm.
Perímetro = 10 + 3 + 10 + 3
Perímetro = 26 cm
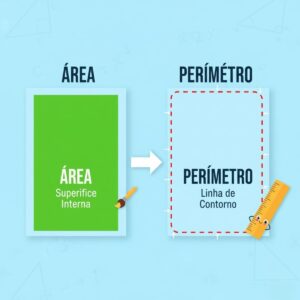
Área: A Lógica da Superfície
Agora, vamos à Área. Se o perímetro é a cerca, a área é o gramado dentro do terreno. É a medida de toda a superfície que a figura ocupa.
A área é uma medida bidimensional (comprimento x largura), por isso usamos unidades “quadradas”, como centímetros quadrados (cm²), metros quadrados (m²) ou quilômetros quadrados (km²).
Exemplo 1: Quadrado (Lado x Lado)
Um quadrado com lado de 5 cm.
Área = 5 x 5
Área = 25 cm² (Note a unidade: “centímetros quadrados”)
Exemplo 2: Retângulo (Base x Altura)
Um retângulo com base de 10 cm e altura de 3 cm.
Área = 10 x 3
Área = 30 cm²
O Caso Clássico de Confusão: Retângulo vs. Quadrado
Observe nossos dois exemplos. O retângulo (Perímetro = 26 cm) tem um contorno maior que o quadrado (Perímetro = 20 cm).
Contudo, o retângulo (Área = 30 cm²) também tem uma superfície maior que o quadrado (Área = 25 cm²). Isso nem sempre é verdade! É perfeitamente possível ter uma figura com perímetro maior, mas área menor. A lógica é que as medidas são independentes.

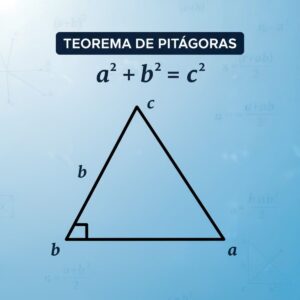
E o Triângulo? A Lógica é a Mesma.
Perímetro do Triângulo:
A lógica não muda. É o contorno. Basta somar os três lados.
Se um triângulo tem lados medindo 5 cm, 7 cm e 8 cm.
Perímetro = 5 + 7 + 8 = 20 cm.
Área do Triângulo: (Base x Altura) / 2
Aqui a lógica é um pouco diferente. Um triângulo é, essencialmente, metade de um retângulo ou paralelogramo.
Por isso, calculamos a área como se fosse um retângulo (Base x Altura) e, em seguida, dividimos o resultado por 2.
Atenção: A “altura” do triângulo é a linha reta do vértice mais alto até a base, formando um ângulo de 90º (não a medida do lado inclinado).
Conclusão: Comprimento vs. Superfície
Portanto, a diferença lógica entre área e perímetro é simples:
- PERÍMETRO = Contorno. A soma dos lados. Medida de comprimento (cm, m).
- ÁREA = Superfície. O preenchimento. Medida de superfície (cm², m²).
Nunca mais confunda os dois. Ao ler um problema, pergunte-se: “Estou calculando o contorno ou o preenchimento?”.
A Matemática é a linguagem do universo, vamos dominá-la!