Teorema de Pitágoras: Mais que a²+b²=c² (A Lógica dos Triângulos Retângulos)

Se existe uma fórmula matemática que quase todos já ouviram falar, é o Teorema de Pitágoras: a² + b² = c². No entanto, muitos decoram a fórmula, mas falham em aplicá-la, pois não compreendem a lógica por trás dela.

Este teorema é a ferramenta mais poderosa da geometria plana e a base para a trigonometria. Portanto, hoje vamos dissecar não apenas a fórmula, mas a lógica de quando e como usá-la corretamente.

O Pré-requisito Lógico: O Triângulo Retângulo

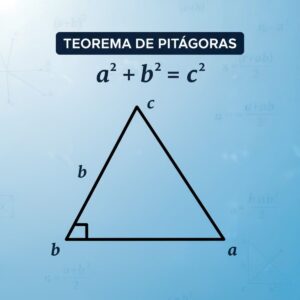
Primeiramente, o ponto mais importante: o Teorema de Pitágoras SÓ funciona em um tipo específico de triângulo: o **Triângulo Retângulo**.

Um triângulo retângulo é qualquer triângulo que possui um ângulo reto, ou seja, um “canto” perfeito de 90º (como o canto de uma folha de papel).

Antes de usar a fórmula, você deve nomear os lados desse triângulo:

• Catetos (a e b): São os dois lados que formam o ângulo reto.
• Hipotenusa (c): É o lado oposto ao ângulo reto. É sempre o maior lado do triângulo.

Identificar a hipotenusa é o passo mais crucial. Se você errar isso, todo o cálculo falhará.

A Fórmula: O que a²+b²=c² Realmente Significa?

A fórmula (a² + b² = c²) pode ser lida em português como:
“A soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.”

Vamos traduzir isso. **Pense fora da caixa e resolva o problema** visualizando as áreas. Se você desenhar um quadrado em cada lado do triângulo:
A área do quadrado no cateto ‘a’ (que é a²) somada com a área do quadrado no cateto ‘b’ (que é b²) terá exatamente a mesma área do quadrado desenhado na hipotenusa ‘c’ (que é c²).

É uma relação de áreas, o que é uma lógica muito mais profunda do que apenas uma fórmula.

Exemplo 1: Descobrindo a Hipotenusa (O Cálculo Direto)

Vamos usar o triângulo retângulo mais famoso: seus catetos medem 3 cm e 4 cm. Qual o valor da hipotenusa (x)?

Passo 1: Identificar os lados.
Cateto (a) = 3
Cateto (b) = 4
Hipotenusa (c) = x (é o valor que queremos encontrar)

Passo 2: Aplicar a fórmula.
a² + b² = c²
3² + 4² = x²

Passo 3: Resolver a potência.
9 + 16 = x²
25 = x²

Passo 4: Isolar o ‘x’ (operação inversa).
A operação inversa de “elevar ao quadrado” é a “raiz quadrada”.
x = √25
x = 5 cm

Exemplo 2: Descobrindo um Cateto (O Erro Comum)

Agora, um desafio diferente. A hipotenusa mede 10 cm e um dos catetos mede 8 cm. Qual o valor do outro cateto (x)?

Passo 1: Identificar os lados.
Cateto (a) = 8
Cateto (b) = x
Hipotenusa (c) = 10 (Note que o 10 é a hipotenusa, o lado maior!)

Passo 2: Aplicar a fórmula.
A hipotenusa (10) deve ficar sozinha do lado direito do “=”.
a² + b² = c²
8² + x² = 10²

Passo 3: Resolver a potência.
64 + x² = 100

Passo 4: Isolar o ‘x’ (como em uma equação de primeiro grau).
x² = 100 – 64
x² = 36

Passo 5: Operação inversa (raiz quadrada).
x = √36
x = 6 cm

O erro comum seria somar 8² + 10². Lembre-se, a hipotenusa é o resultado, não parte da soma.

Conclusão: A Ferramenta Mestra da Geometria

Portanto, o Teorema de Pitágoras é muito mais que uma fórmula. É a regra lógica que governa todos os triângulos retângulos. Ele nos permite descobrir uma distância desconhecida usando outras duas, sendo a base para a navegação, a engenharia e, claro, o próximo passo da matemática: a Trigonometria.

A Matemática é a linguagem do universo, vamos dominá-la!